平成30年度の都立戸山高校数学を時間を計って解いてみました。
問題は戸山高校のサイトからダウンロードできます。
(噂には聞いていましたが)解いてみた感触はやはり、かなり簡単でした。今回は検算しつつとても慎重に解いたのですが、大問1に10分、大問2~4にそれぞれ5分ずつの計25分で解き終わり、満点でした。入試本番で満点を取った子もいたのではないでしょうか?
2018年10月現在、平成30年度の戸山高校自校作成問題の数学の受検者平均点はネット上には見当たりませんでしたが、下記掲示板などを参考に考えると、おそらく69点くらいだったのではないかと思います。(自校作成校の数学で平均点70点台は信じがたいので、ギリギリの69点としました笑)
https://www.zyuken.net/school_page/11310421217/bbs_query/%E3%83%9C%E3%83%BC%E3%83%80%E3%83%BC/
大問1(小問集合)
目標解答時間:13分 難易度:普通
作図が簡単だったので、25点中20点以上は取りたい。

〔問2〕 工夫して(x+2をXと置いて)計算していきます。x+2をXと置いた式が因数分解できず、解の公式を使う必要があります。それでも、普通に展開してから解の公式を使うよりは速いでしょう。
〔問4〕 やや難。数え漏れが起こりやすく、難問というわけではないものの、大問1の中では特に慎重を要する問題でした。
[解答]
n=60, 120, 180で点Pが点Aの位置に戻る。n=60を実現するのは(2, 5, 6), (3, 4, 5)とその並べ替え。n=120は(4, 5, 6)とその並べ替え。n=180は(5, 6, 6)とその並べ替え。6 + 6 + 6 + 3 = 21通りで、21/216 = 7/72。
〔問5〕 易。都立共通問題レベルの簡単な作図でした。解けなかった人は、垂直二等分線と角の二等分線の作図方法と性質をおさらいしておきましょう。30度、45度、60度、90度の作図、正三角形の作図、円が与えられているときのその中心の作図なども、自校作成校の作図ではよく題材となります。もれなく覚えておきましょう。
[解答]
線分ACの垂直二等分線を作図し、線分ACと垂直二等分線の交点Pを中心とし、半径PAの円を描く。
大問2(関数)
目標解答時間:10分 難易度:やや易
25点満点もしくは、1問ミスまでを狙いたい。
二次関数と反比例という珍しい組み合わせの出題。戸山ではH29, H25でも反比例が出題されており、出題頻度は高めです。
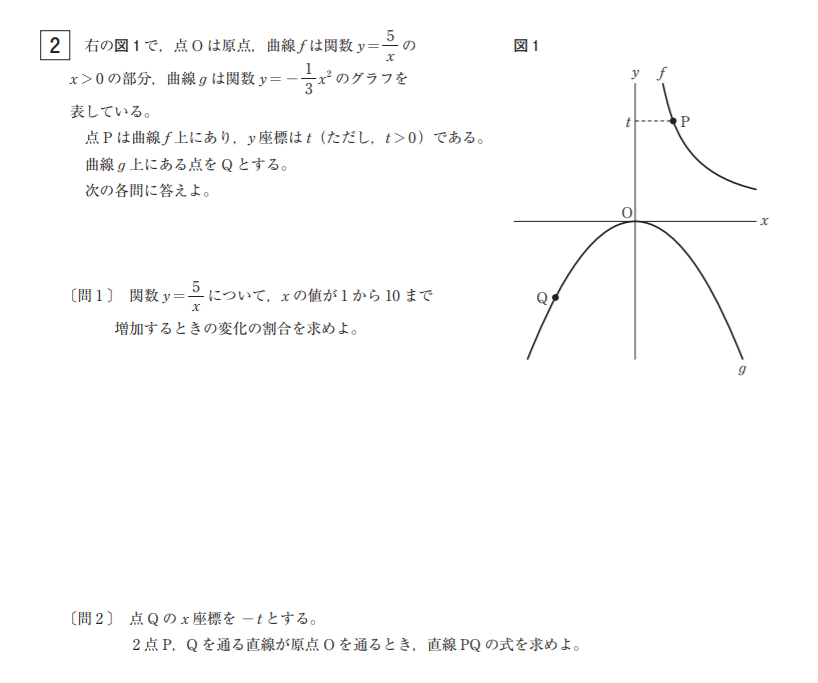
〔問1〕 易。下のような表を書いて、(yの増加量)/(xの増加量)を計算することで解けます。反比例の関数で変化の割合を求める問題は不慣れかもしれませんが、変化の割合の意味がきちんと理解できていれば特に問題はないはずです。
| x | 1 → 10 |
|---|---|
| y | 5 → 1/2 |
変化の割合の数値を求めたら、問題用紙のグラフ上に2点を書き込んでみて、正負や傾きの度合いなど、最低限のチェックはしておきたい。
〔問2〕 普通~やや易。条件を用いてtを消去する問題であることを見抜けるかどうか。
[解答]
\(Q \left( -t, – \displaystyle \frac{1}{3}t^2 \right)\)と原点\(O \left( 0, 0\right)\)から直線\(QO\)の式を求めると、\(y = \displaystyle \frac{1}{3}tx\)となる。
\(P \left( \displaystyle \frac{5}{t}, t\right)\)が直線\(QO : y = \displaystyle \frac{1}{3}tx\)上にあることから、代入して\(t = \displaystyle \frac{1}{3}t \times \displaystyle \frac{5}{t}\) これを解いて\(t = \displaystyle \frac{5}{3}\)
これを直線\(QO : y = \displaystyle \frac{1}{3}tx\)に代入し、\(y = \displaystyle \frac{5}{9}x\)を得る。

〔問3〕 易。中点の座標が与えられていることからtの値を求め、三角形の面積を求める定型的な問題でした。辺RPがx軸に平行であることから求積も容易です。熱心な受験生であれば都トレや過去問で類似問題をたくさん解いているはずなので、戸山の受験生としては絶対に落としてはいけない問題です。
この問題は記述式のため学校解答が解説となっておりますので、解説は省略します。
大問3(平面図形)
目標解答時間:10分 難易度:易
25点満点もしくは、1問ミスまでを狙いたい。
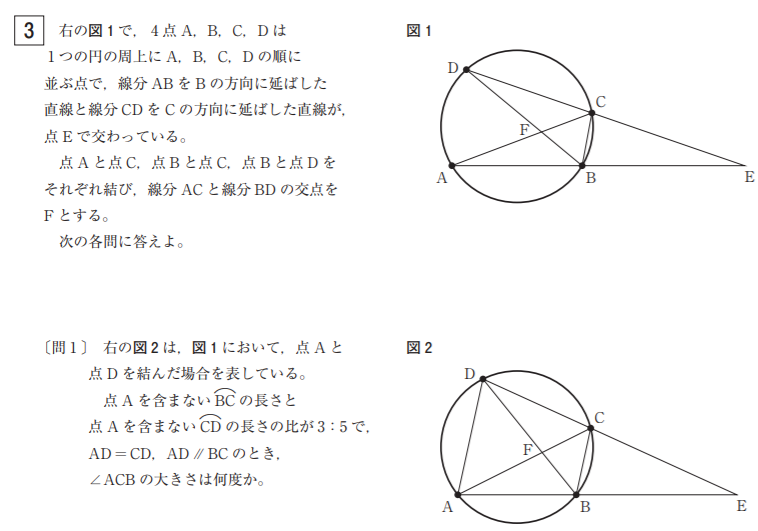
〔問1〕 やや易。「円1周分の円周角は180度であり、円周角は弧の長さに比例する」ことは、標準レベルの生徒ではなかなか活用できない子も多いですが、戸山の受験生としてはキッチリとおさえておきたいところ。
\(AD/\!/BC\)から\(\stackrel{ \Large \frown }{ AB } = \stackrel{ \Large \frown }{ DC } \)となることがよく納得できない人は、自分で円と平行線をいろいろなパターンで書いてみよう。
[解答]
\(AD=CD, AD/\!/BC\)から、\(\stackrel{ \Large \frown }{ BC } : \stackrel{ \Large \frown }{ CD } : \stackrel{ \Large \frown }{ AD } : \stackrel{ \Large \frown }{ AB } = 3 : 5 : 5 : 5\)となる。
よって、\(\stackrel{ \Large \frown }{ AB }\)に対する円周角である\(\angle ACB\)は、\(180 \times \displaystyle \frac{5}{18} = 50^{ \circ }\)

〔問2〕 易。都立共通レベルなので、ここは落としたくないです。証明なので、解答は学校解答をご参照ください。
〔問3〕 やや易。「等高ならば底辺の比は面積の比」を用いる類題演習を徹底的にやっていれば、かなり簡単に感じるはずの問題です。
[解答]
辺の比を整数で表していく。
\(AB : BG : GE = 6 : 2 : 3\)
\(AB : BG = 6 : 2\)から、\(BF : GC = 9 : 12\)
\(GE : BG = 3 : 2\)から、\(GC : BD = 12 : 20\)かつ\(EC : CD = 3 : 2\)
よって\(BF : FD = 9 : 11\)
以上で必要な辺の比が分かる。あとは「等高ならば底辺の比は面積の比」を順々に適用していくと、結果的に以下のようになる。
\(\triangle DFC : \triangle BCF : \triangle GEC : \triangle BGC : \triangle ABF = 11 : 9 : 18 : 12 : 27\)
よって \(\triangle ACE : \triangle BCF = 66 : 9 = 22 : 3\)
よって\(\displaystyle \frac{22}{3}\)倍。
大問4(立体図形)
目標解答時間:15分 難易度:やや易
問1と問2でのミスはなるべく避けたい。問3はそれほど難しくないので、数学が得意な生徒であれば完答を目指してもいいレベルだと思います。
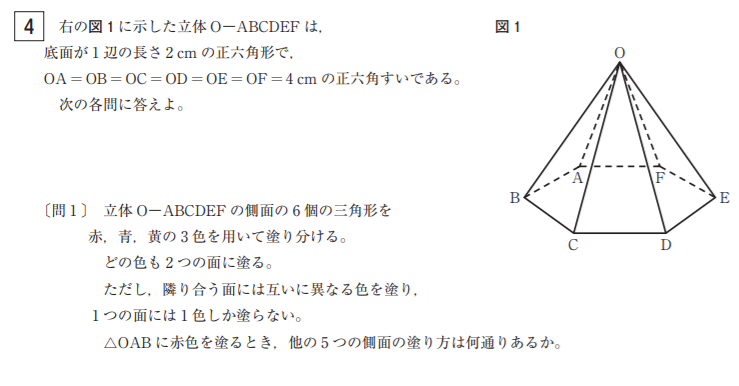

〔問1〕 やや易。
[解答]
赤、青、黄をr, b, yする。△OAB-△OBC-△OCD-△ODE-△OEF-△OFAの順に塗っていくことを考える。△OBCをbとする塗り方は以下の4通り。△OBCをyとしても同様に4通りあるので、計8通り。
| △OAB | △OBC | △OCD | △ODE | △OEF | △OFA | |
|---|---|---|---|---|---|---|
| r | b | r | y | b | y | ① |
| y | b | r | y | ② | ||
| r | b | y | ③ | |||
| y | b | ④ |
〔問2〕 易。底面積となる正六角形の求積は、正六角形を正三角形6個に分割して行う。あとは高さを三平方で求めるだけの問題。

〔問3〕 普通。戸山の最後の問題にしては割と易しめ。時間が足りない場合には、せめてPQとDEの長さには触れておくこと。2点くらいはもらえるかもしれません。
学校解答が解説になっているので、解答は省略します。
